Importance of Squares And Square Roots
In mathematics, squaring of a number is easy to understand. Squaring a number means multiplying the original number by itself. Squaring is expressed in mathematical terms by putting ‘2’ to the power of a number you are squaring to designate that it is multiplied 2 times. For example:
4×4 = 42 = 16
The application of squares in maths we will see commonly in algebra. Most of the algebraic identities are based on squares, such as:
(a+b)2 = a2 + b2 + 2ab
(a-b)2 = a2 + b2 – 2ab
etc.
In the same way, squares concept is used in finding the roots of quadratic equations. The most famous of the method is completing the square. This is a method of rearranging the terms into a complete square in such a way that, the form of the equation is changed so that the left side is a perfect square trinomial. Here are the steps for this method.
Suppose px2 + qx + r = 0 is a quadratic equation. Then follow the provided steps for solving the equation using completing the square method.
- Write the quadratic equation in such a way that ‘r’ is on the right side.
- If ‘p’ is not equal to 1, then divide the complete equation by ‘p’, such that co-efficient of x2 is 1.
- Now add the square of half of the co-efficient of term-x, (q/2p)2, on both the sides.
- Factorise the left side of the equation as the square of the binomial term.
- Take the square root on both sides.
- Solve for variable x and find the roots.
Hence, you will get the roots of the equation.
The square root is more complicated to understand. When we find the square root of a number we actually find out the original number that was squared. So the square root of 16 is 4. Squares and square roots usually come in pairs. In this case, 4 squared is 16 and the square root of 16 is 4.
Squares are always simple to calculate but finding a square root is complicated. Square roots are compounded because the square root of a number is usually a long decimal number. The square root of 4 (2 x 2), 9 (3 x 3) or 256 (16 x 16) are easy to find because they are perfect squares. But what about the square root of 2? The square root of 2 is 1.414. You can verify it by squaring 1.414.
Imagine how complicated the square root of a huge number becomes! There are various methods for estimating square roots but you will normally use a table or calculator when you require to find a square root.
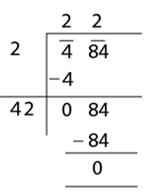
The square root of different numbers can be estimated using prime factorisation or long division method. It is easy to find the square root using factorisation of numbers into their prime factors. But for large numbers and imperfect squares, it is more preferred to use long division method to take out the square root. An example of an estimation of the square root of 484 is given below:
One reason why square root is more important is that it is used all the time by scientists, engineers and even people who work in factories.